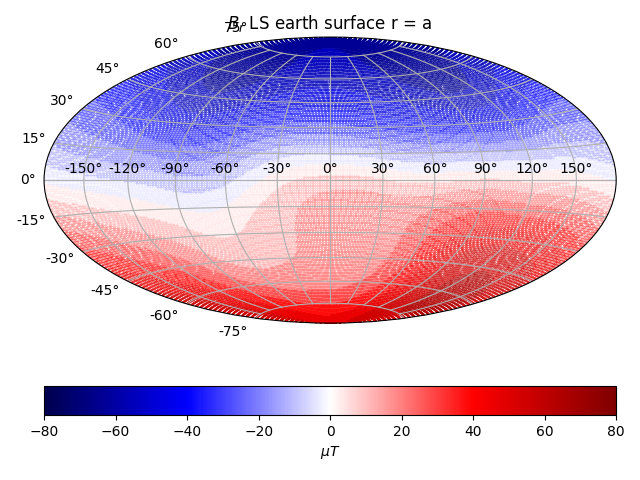
Magnetic field data captured by SWARM satellite. Downward continuation Robust estimation, iterated IRLS Overdetermined system. Conditioning numbers. The data consists of around 7500 observations, made in 2014, by a high-altitude satellite. The field data will be used to fit a model for the core surface boundary. This procedure includes downward continuation, which introduces instability and amplifies short wavelengths and observation noise. Thus regularization is required. We can start off with a simple inversion method, assuming gaussian noise and thus using L2-norm on the misfit, with L2-norm on the model. This is the classical Tikhonov (Ridge regression special case) method. Then we can try combinations of L1 norm and L2 norms on model and misfit. Around 97% of the magnetic field measured on Earth originates from internal sources. The core is too hot to sustain a permanent magnet, and instead much more difficult dynamics are at play, involving fluid dynamics along with the rotation of Earth. Note that this is a model for the radial field alone, where the magnetic field consists of also two angular directions. The radial magnetic field data can be seen below
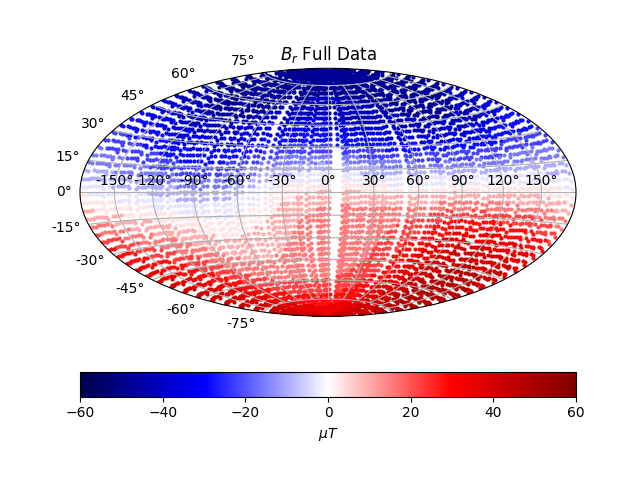
As can be seen from the data, putting aside errors, the radial magnetic field of Earth is largely a dipole, as from a north-south bar magnet. The north pole is the magnetic south pole, and vice verca. That situation changes with time however, as the field reverses on large timescales. The predicted field is squished towards zero, leaving the amplitudes smaller, and also create a strong bias beyond any physically reasonable solution.
From Maxwell's equations, the curl of the magnetic field is zero in a region free from current sources, or constant electric field, The model can be derived from some simple physical considerations and assumptions.
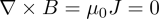
Magnetic measurements on the satellite are done with shielding from electronic, to shield the measurement device as much as possible from the electromagnetic noise from the satellite itself. For zero curl, the field can be written as gradient of a potential field,

The magnetic field is divergence free,
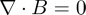
And so we can arrive at Laplace's equations
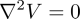
The parameters of the model are the g's and h's. For a SH model of degree n = 20, without intercept, there will be 440 model parameters. About 20 degree SH model is reasonable for a model at the surface of Earth. Only internal sources are modelled, i.e magnetic disturbances from the ionosphere, the influence of the sun etc. is not modelled, but will be present as variance in the data. With up to 7561 data points we thus have an overdetermined system. For computational efficiency, only around 750 points will be used, at the cost of more uncertainty in the results. The sum of spherical harmonics, with radius coefficients, will make up the design matrix G, that is used in the inverse steps to find the model m, which consits of the g's and h's. The radius factor is seen with reference from the surface of earth, with a = 6371km, and while the data is collected at around 6800km by the sattelite, and also consideration of the field at the core-mantle boundary will be given, which is at a radius of 3480km. Thus the inverse problem uses both downward continuation and upward continuation. Downward continuation to the CMB is an unstable process, which gives weight to higher frequencies, as will be seen in some of the methods.
Least Squares regression
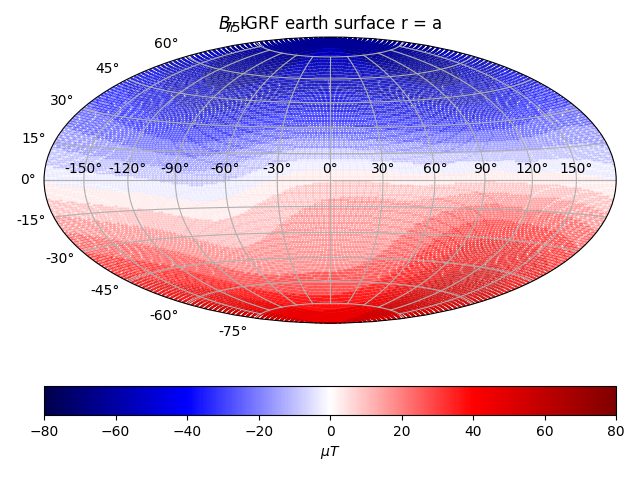
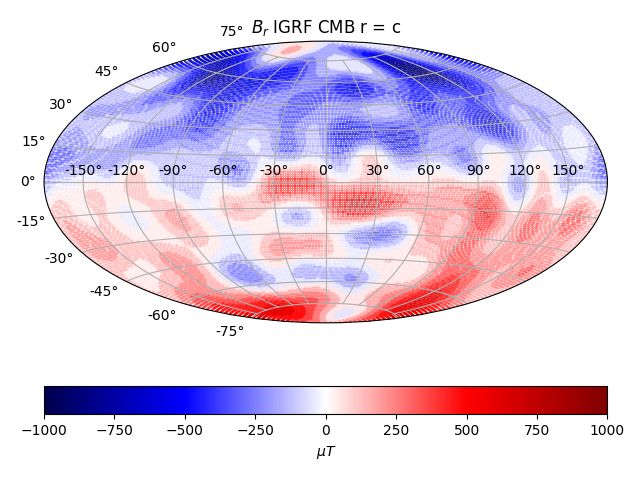
The least squares solution is prone to outliers in data and variance in estimated model parameters. In the variance-bias tradeoff framework, the LS method puts no bias on the model parameters and has a high variance. We can compare the LS solution with IGRF
Earth Surface Least Squares
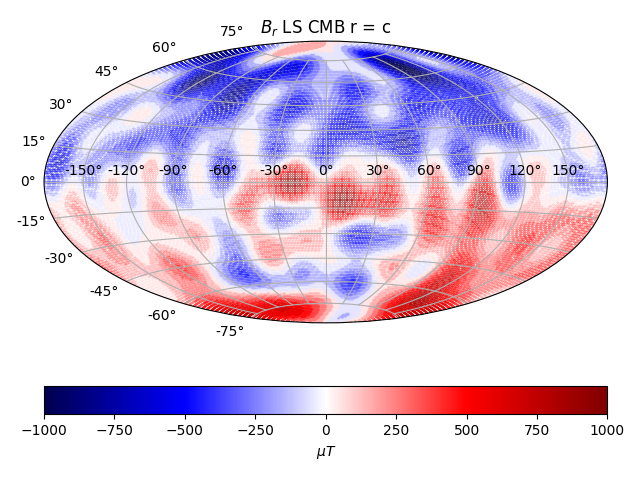
CMB Core-Mantle Boundary Least Squares
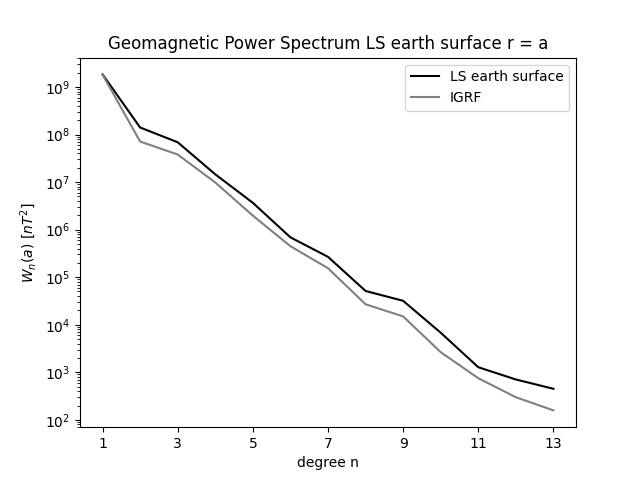
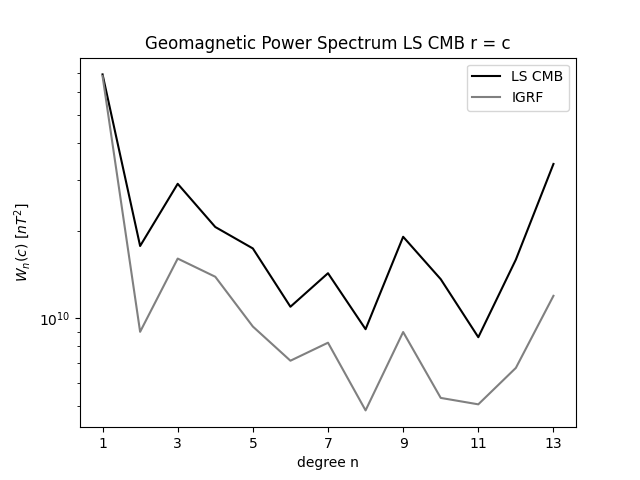
Geomagnetic Power Spectrum Least Squares
Ridge Regression - L2L2 norm
One of the earliest methods in regularized regression, in reducing variance, is the Ridge regression. To reduce variance of predictions and model parameters, we can put a penalty on the sum of squared parameters, next to the penantly on misfit. It can be expressed in the lagrangian form as
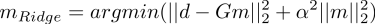
The advantage to the Ridge regression is the simple analytical solution, which can be cleanly expressed, without having to use iterative methods
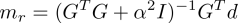
The predicted space data and CMB data for a particular regularisation parameter is chosen below.
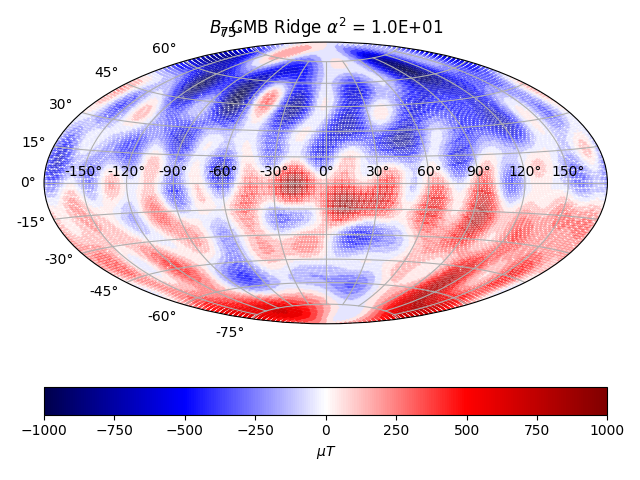
The solution at satellite height matches the data well visually, at least. At CMB level, the solution makes no sense, with higher frequencies dominating. It looks physically unreasonable, knowing what the surface and satellite height field looks like. The CMB field should still largely be dominated by a dipolar mode.
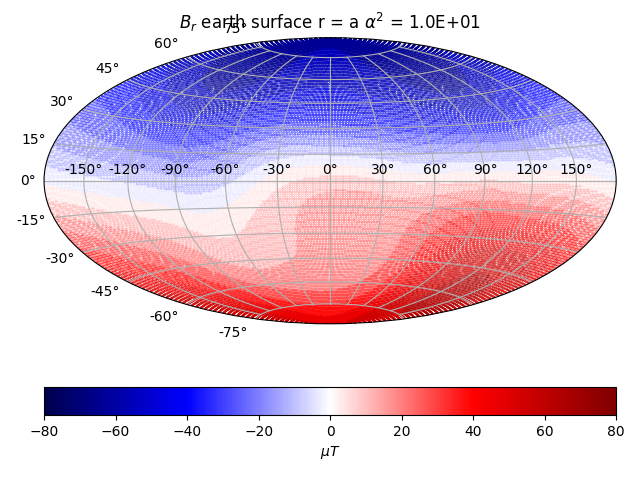
Earth Surface Ridge Solution

CMB Core-Mantle Boundary Ridge solution

The Ridge regression is fast to compute, since we do not need to iterate and converge. We can try for many parameters, and over a very long range.
Geomagnetic Power Spectrum Ridge Solution
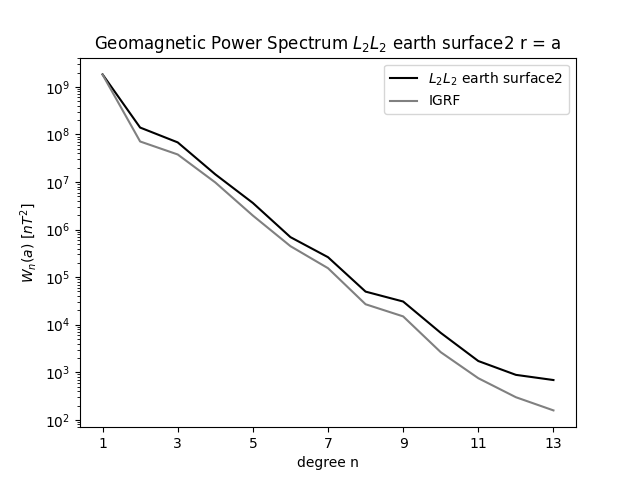
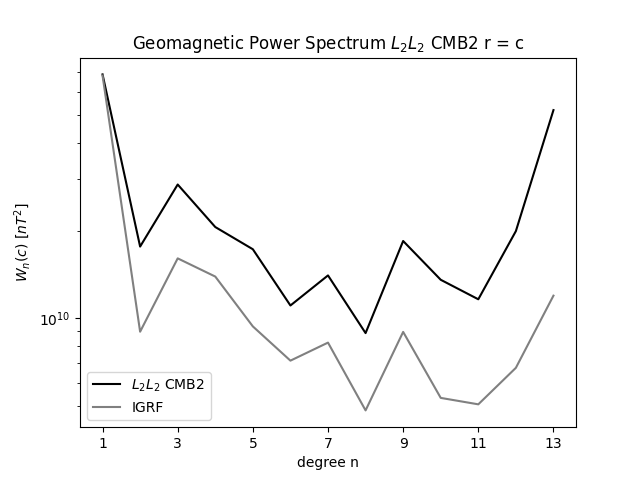
It's best to downward continue the Earth Surface field at to the core-mantle boundary, if there is no field generated in the mantle and the curst. (Lowes,1974) I.e no sources of Br in between. There are small but significant sources to the surface field, from magnetized crustal rocks. We can expect the crustal field to exist mostly of higher harmonics, due to its shallow origin. Early estimates showed the crustal field to mostly show itself from n = 25 and upwards, to e.g n = 500. We mostly expect the core field to be flat or slowly decreasing up to n = 10, at the core field, corresponding to nearly a 'white' spectrum from the sources at radius 0.47a, with maybe a slight increase for n = 2, due to a deeper dipole source at 0.35a The earth surface spectrum decreases up to between n = 14 to 20, with main contributions from the core field. The ES spectrum then stays nearly flat from n = 20. And the core field is greater than the crustal field to at least n = 11, while the crustal field likely has very low contribution for small n. According to (Langel & Estes 1982) we see to distinct slopes at Earth Surface magnetic field spectrum, with a distinct change at n = 14. The spectrum before that comes mostly from core field sources, and the spectrum after n = 15 from crustal sources. It is difficult to observe the core field after n = 14, because the crustal field obscures it. External sources include ionosphere and magnetosphere. The Earth Surface spectrum, the dipole term stands way higher than the rest, and a break near n = 14. The higher degrees are not due to noise in data, but carry actual meaningful physical information. The crustal field thus puts a limitation on our ability to estimate the core field, mostly for higher frequencies. The core spectrum should decrease slightly up to n = 14, and after that, increase fast. For n = 13 and 14, the crustal field still contributes a lot to the core spectrum. The power spectrum for the first 10 degrees is not too bad. However the power spectrum does tend to rise for larger n.
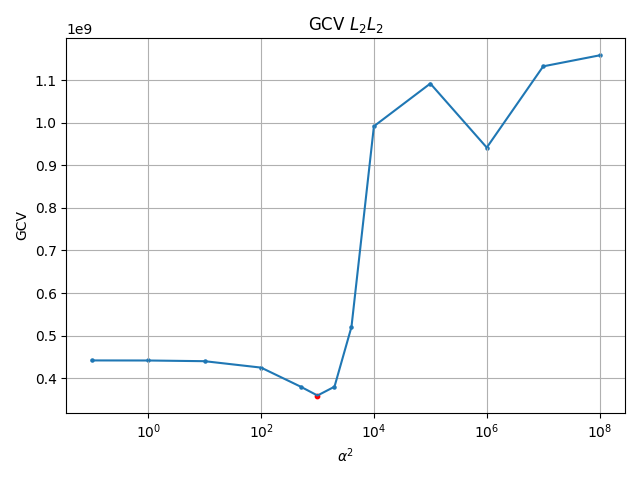
Generalized Cross Variance can be used to be pick regularization parameter. It does seem to choose a parameter slightly too high, which leads to unphysical solutions. So I picked a parameter slightly less than what GCV suggested.