The slug test is a (rather crude) test for transmissivity and storage coefficients for aquifiers. . Basically, we are trying to determine 2 parameters. Storage is between 0 and 1. We quickly fill a well with water, and measure the head in another nearby well. There are practical caveats to consider with the slug test and its accuracy, as there are with other aquifier tests, but it's always interesting to take the inverse problem formulation as an educational example.
The water head h is described by
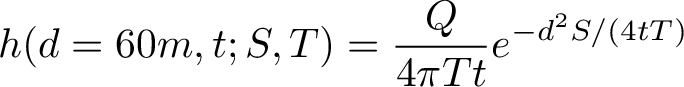
Here, t is time, and d = 60m is distance from the point that we fill with water, to the point that we measure the head. Thus we are basically measuring the response to a spike input of water at a point in the aquifier.
Since it's a nonlinear regression problem, we will iterate using Gauss-Newton method starting from some initial feasible guess on T and S coefficients.
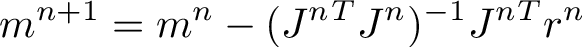
The residuals is given as usual by
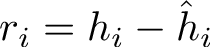
The derivatives for the Jacobian,
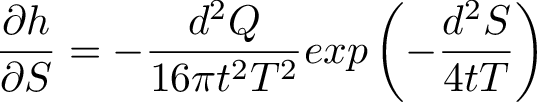
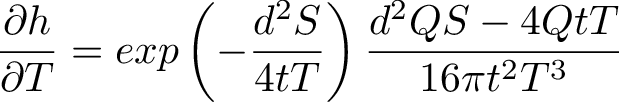
The derivatives will be updated at each iteration step. The jacobian has 2 columns for the 2 unknown coefficients, and the rows come from each datapoint, giving n rows in the Jacobian.
We iterate m, which is the vector for model parameters S and T:
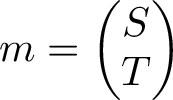
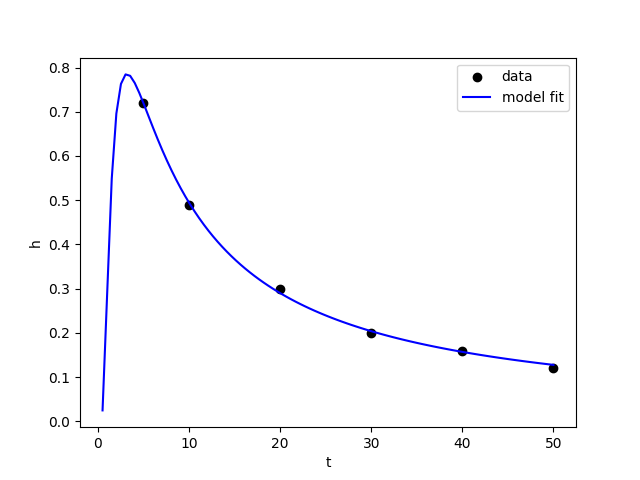
Example data
Example from chapter 7 from the reference book. The synthetic data consists of 6 (t,h) points. The curve is basically fitted to the data points, which are measurements recorded at a d = 60m at t = 5,10,20,30,40,50s
The solution as given by the algorithm noted above is given here, along with contours, giving some indication of confidence/uncertainty.
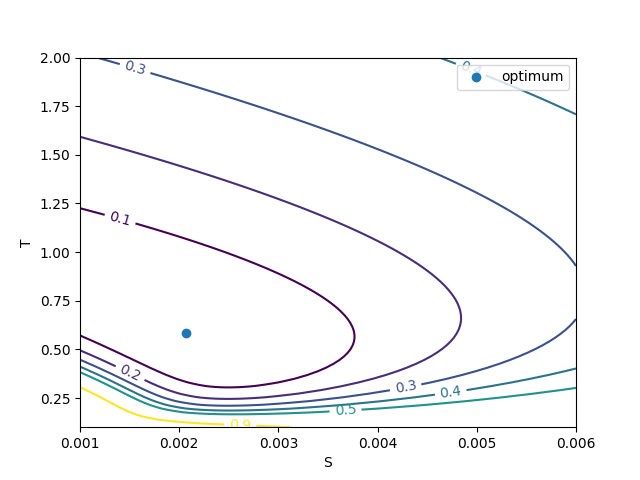
A peak can be seen around S = 0.002 and T = 0.65. Close to the peak, the contours are approximately elliptical.
References
Richard C. Aster, Brian Borchers, Clifford H. Thurber - Parameter Estimation and Inverse Problem (2ed)